¡Hola humanos! ¿Cómo están? Hoy aprenderemos todo lo que se necesita para conocer y resolver ecuaciones de primer grado.
Primero, ¿qué es una ecuación?
Una ecuación es una proposición lógica, algo así como una oración o frase, que puede ser cierta o falsa dependiendo de los números con los que la evaluemos. Una proposición lógica de este tipo sería por ejemplo:
$2x+4=16$
Que simplemente nos propone que el doble de un número (al que llamaremos x) más 4, es igual a 16. Si razonamos un poco, llegaremos a la solución x=6, porque:
$2(6)+4=16$
$12+4=16$
Y como 12+4=16, entonces el valor x=6 hace que la proposición sea verdadera. Cualquier otro número que asignemos a x provocará que la proposición sea falsa, como por ejemplo vamos ahora a sustituir x=3 en la ecuación:
$2(3)+4=16$
Que es una proposición falsa porque la proposición lógica sería:
$6+4=16$
Y como sabemos 10 no es igual que 16.
Entonces, una ecuación puede considerarse como un enunciado que puede ser falso o verdadero, dependiendo del número que sustituyamos en el lugar de la incógnita.
¿Cuáles son los elementos de una ecuación de primer grado?
Todas las ecuaciones tienen tres elementos básicos: el miembro izquierdo, el signo de igualdad, y el miembro derecho:
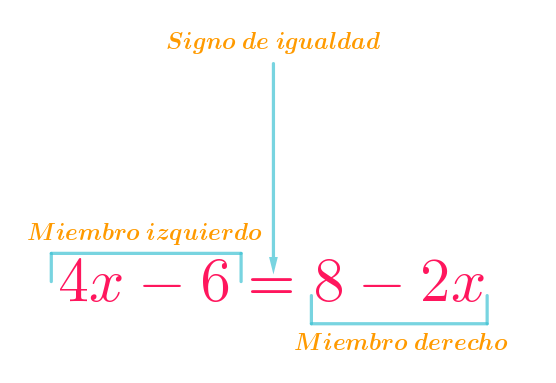
Cada miembro está formado de sumas, restas, multiplicaciones, divisiones o más operaciones entre los términos de cada miembro, que pueden tener incógnitas o no.
¿De qué trata resolver una ecuación de primer grado?
Resolver una ecuación entonces consistirá en encontrar el, o los números que hagan que la proposición lógica sea verdadera, humanos. Cuando decimos que es de primer grado, nos referimos al mayor exponente que tenga un término cualquiera de la ecuación, que contenga una incógnita; por ejemplo, la ecuación:
$2x+5=4-3x$
Es de primer grado porque los términos 2x y -3x tienen exponente uno. La ecuación:
$3{{x}^{2}}-6x=-12$
Es de grado 2 porque el exponente de mayor grado es 2.
Las ecuaciones de primer grado pueden tener una solución, las de segundo grado hasta dos soluciones, las de tercer grado hasta 3, las de cuarto pueden tener hasta… bueno, así podríamos seguir.
¿Y cómo se resuelven?
Para resolver una ecuación vamos a imaginarla como una balanza en equilibrio, en la que cada uno de sus platos es uno de los miembros de la ecuación: podemos agregar o quitar peso, pero siempre en los dos miembros para no alterar su equilibrio, si sumamos o restamos cualquier número en el miembro izquierdo, debemos hacerlo también en el derecho. Si multiplicamos o dividimos en el miembro derecho, también debemos hacer lo mismo en el miembro izquierdo.

La idea es sumar, restar, multiplicar o dividir términos o números que nos lleven a encontrar el valor de la incógnita. Como ejemplo vamos a resolver la ecuación \(8-2x=x-1 \). Vamos a mover todos los términos con la incógnita x al miembro izquierdo y a los términos independientes al derecho. Iremos poco a poco y haremos esto primero con los términos con incógnita. Vamos a sumar -x (o a restar x, es lo mismo), tanto en el miembro derecho como en el izquierdo:
$8-2x-x=x-x-1$
Hicimos esto porque así eliminamos la incógnita x del miembro derecho; que puede verse si desarrollamos las operaciones:
$8-3x=-1$
Si observan humanos, de aquí viene lo que conocemos como «pasar el término al otro lado con el signo contrario». Vamos ahora a repetir este procedimiento para mover el 8 al miembro derecho; lo haremos restando:
$8-8-3x=-1-8$
$-3x=-9$
Y como último paso vamos a dividir entre -3 para que x en el miembro izquierdo quede libre:
$\frac{{-3x}}{{-3}}=\frac{{-9}}{{-3}}$
$x=3$
También de estos pasos es de donde viene el famoso «si está multiplicando, pasa dividiendo». La mejor forma de dominar este proceso es repitiéndolo, les recomendamos resolver muchos ejercicios. Cuando lo dominen, ya se podrán saltar pasos.
Es todo en este post humanos, los michis y su esclavo esperamos que les sea útil, cuídense y practiquen.
