¡Hola humanos :3! Ahora toca aprender en qué consiste la representación gráfica de funciones. Para poder hacerlo, les invitamos a que visiten la entradas sobre localización de puntos en el plano cartesiano y sobre lo básico que necesitan saber sobre funciones.
Al observar, es fácil notar que entre un par ordenado y un punto hay mucho parecido: los puntos se definen como parejas de coordenadas de la forma $ P\left( {x,y} \right)$ y los pares ordenados son parejas de números que se toman de entre los elementos de dos conjuntos, y que tienen la forma $ \left( {x,f\left( x \right)} \right)$. Desde el punto de vista matemático son conceptos diferentes pero muy parecidos. ¿Y qué pasaría si a los pares ordenados de una función los ubicamos en un plano cartesiano, tal como si fueran puntos? Lo que obtenemos es la gráfica de la función a la que pertenecen estos pares.
Veamos un ejemplo sencillo: tracemos la gráfica de la función $ f\left( x \right)=2$. Para hacerlo vamos a encontrar algunos pares ordenados de ella. La función es fácil de graficar porque en lenguaje común nos dice que para cualquier valor de $x$, le corresponde siempre el valor $ f\left( x \right)=2$, vamos que si x vale 1, f(x) vale 2, si x vale 2, f(x) vale 2, si x vale 3, f(x) vale 2, y así hasta el fin de los tiempos. Los pares ordenados de esta función se pueden observar de forma sencilla si nos ayudamos de una tabla:
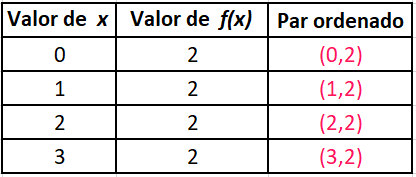
Y si en un plano cartesiano ubicamos estos pares ordenados y los unimos con una línea recta, obtendremos la siguiente gráfica:
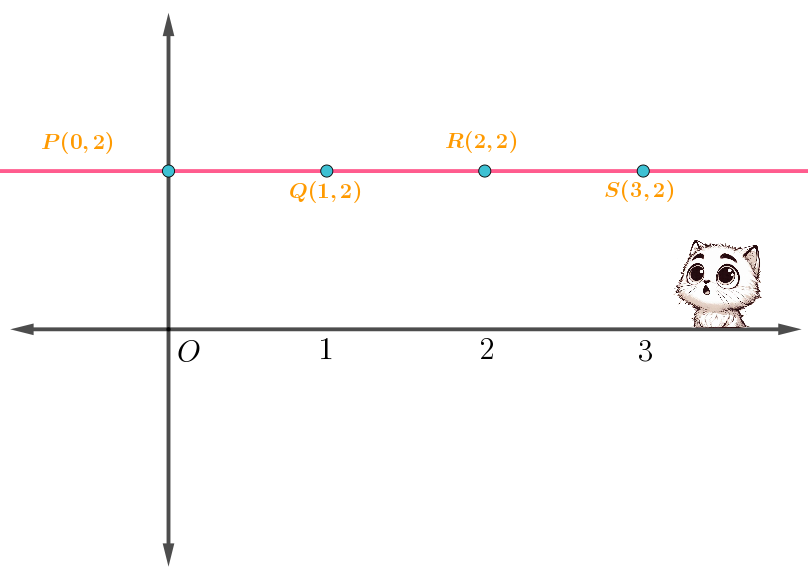
Obtenemos así una línea recta con un ángulo de cero grados con respecto al eje $ x’x$.
Ahora vamos a trazar la gráfica de una función algo más compleja; la de $ f\left( x \right)={{x}^{2}}+3x-1$. En los casos en los que las funciones a graficar sean complicadas, podemos agregar una columna a nuestra tabla, en la que resolvemos las operaciones que nos indica la regla de correspondencia. En este ejemplo la tabla será la siguiente:
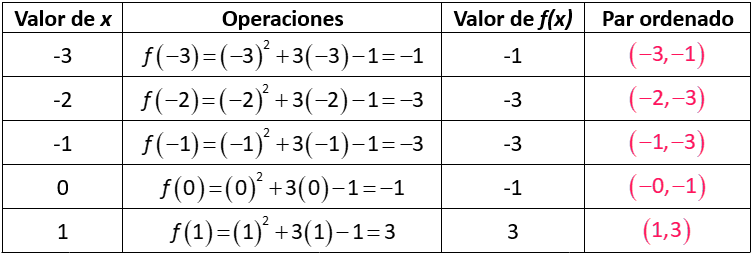
Y la gráfica que le corresponde es esta:
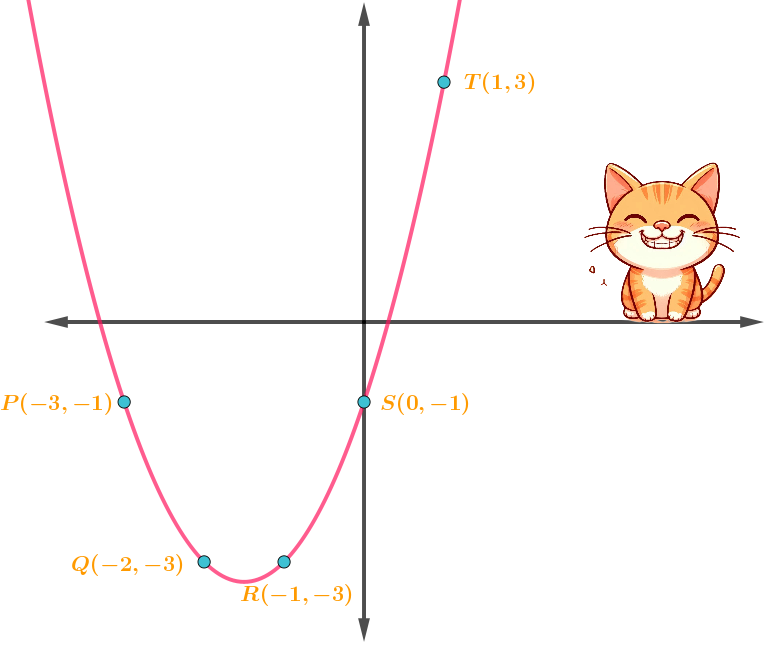
Es común que con solo unos cuantos puntos no nos sea fácil visualizar cómo será la gráfica de una función, El Esclavo les sugiere que encuentren todos los puntos que hagan falta hasta que puedan visualizar bien la gráfica, humanos.
Habrán funciones en las que en algún intervalo haya una discontinuidad, esto de forma muy simplificada quiere decir que en algunas partes, la función no existirá y no tendrá gráfica, esto sucede cuando en la regla de correspondencia sustituimos valores de x que provocan contradicciones matemáticas; por ejemplo, en la siguiente función:
$ f\left( x \right)=\frac{1}{{{{x}^{2}}}}$
Podremos sustituir casi todos los valores de x que se nos ocurran, casi. Un valor de x que no podemos sustituir en esta función es x=0 porque:
$ f\left( 0 \right)=\frac{1}{{{{{\left( 0 \right)}}^{2}}}}=\frac{1}{0}$
Y la división entre cero no está definida porque lleva a algunas contradicciones entre las operaciones de multiplicación y división. La gráfica de la función es la siguiente:
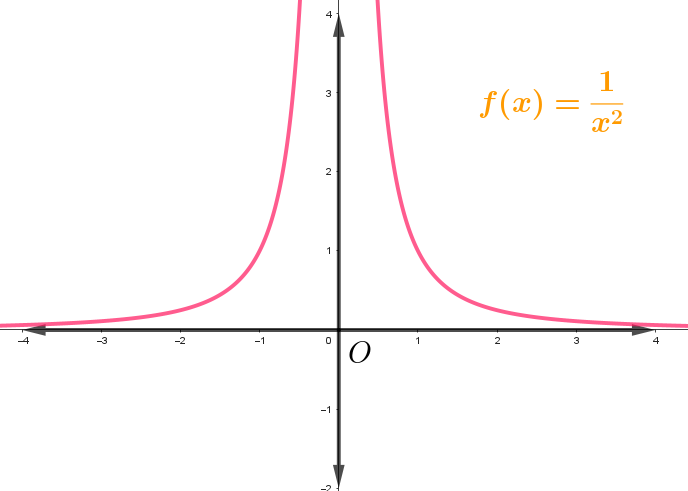
Como se puede ver, la gráfica se interrumpe, esta interrupción (en realidad se llama discontinuidad) nos está indicando que en donde sucede, la función no existe, en este caso en x=0. En general, todas las funciones cuya regla de correspondencia son polinomios, son siempre continuas y estos problemas no se presentan en ellas, pero como en el ejemplo anterior, en el que la función es racional, siempre habrá al menos una discontinuidad. Otras funciones que pueden tener discontinuidades son trascendentes como muchas que incluyen a la razón tangente; o que incluyan logaritmos.
Es todo por el momento humanos, El Esclavo, por orden de sus michis irá subiendo más contenido que les sea útil, ¡Abrazos!
