¡Saludos humanos! Vamos a aprender lo básico sobre los números imaginarios y los números complejos: de dónde surgen, en qué consisten y cómo se representan.
Primero ¿Qué es un número imaginario?
Existe una cantidad enorme de operaciones matemáticas que no tienen solución si intentamos resolverlas con algunos conjuntos de números, por ejemplo, imaginemos por un momento que sólo conocemos los números naturales: $ \mathbb{N}=\left\{ {0,1,2,3,4,5…} \right\}$, y que queremos resolver la resta 5-7; ¿cuál es el resultado si sólo tenemos números naturales? Es claro que sin el conjunto de números adecuado, la resta 5-7 no tiene solución, y por eso a alguien se le ocurrió el conjunto de los números enteros $ \mathbb{Z}=\left\{ {…-4,-3,-2,-1,0,1,2,3,4…} \right\}$, y con ellos ya podemos resolver nuestra resta: 5-7=-2.
La situación con los números imaginarios es muy parecida a la anterior porque fueron inventados para dar solución a un problema que no tiene solución si usamos números reales. El problema que dio origen a los imaginarios involucra potencias y raíces pares (cuadrado de un número y su raíz cuadrada, por ejemplo). Veamos un ejemplo sencillo, con un número cualquiera, al que llamaremos a. Empezamos con los cuadrados de a y de -a:
$ \displaystyle \begin{array}{c}\left( a \right)\left( a \right)={{a}^{2}}\\\\\left( {-a} \right)\left( {-a} \right)={{a}^{2}}\end{array}$
Grandioso. Sabiendo lo anterior, ya podemos razonar que:
$ \displaystyle \begin{array}{c}\sqrt{{{{a}^{2}}}}=a\text{ porque }\left( a \right)\left( a \right)={{a}^{2}}\\y\\\sqrt{{{{a}^{2}}}}=-a\text{ porque }\left( {-a} \right)\left( {-a} \right)={{a}^{2}}\end{array}$
Muy bien, ¿y qué pasa en el siguiente caso?
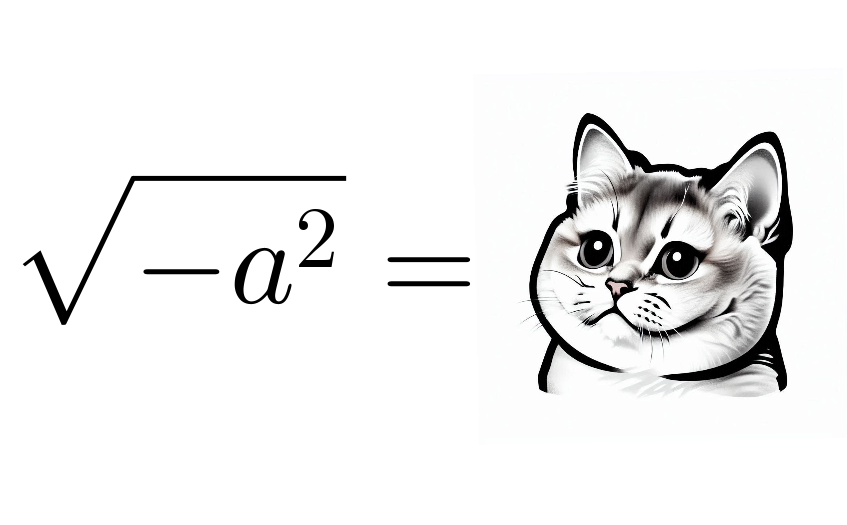
Ya vimos que el cuadrado de un número resulta ser positivo, sea éste positivo o negativo, ¿Entonces qué hace un signo negativo en la raíz cuadrada de $ \displaystyle {{a}^{2}}$? Teniendo solamente a los números reales, esto no tiene solución; pero vamos a hacer algunas cosas; vamos a factorizar -1:
$ \begin{array}{c}\sqrt{{-{{a}^{2}}}}=\sqrt{{\left( {-1} \right)\left( {{{a}^{2}}} \right)}}\\\\\sqrt{{-{{a}^{2}}}}=\sqrt{{-1}}\sqrt{{{{a}^{2}}}}\end{array}$
De esto último, vamos ahora a poner atención en el factor $ \sqrt{{-1}}$ . Este número se conoce como i, y que tiene el valor de:
$ i=\sqrt{{-1}}$
A las raíces de números negativos es a las que se les conoce como números imaginarios. En general, un número imaginario es todo aquel que tiene la forma ai; es decir, un número imaginario es el producto de un número real, por el número i.
¿Y qué tienen que ver los números imaginarios con los complejos?
Un número complejo, comúnmente representado con la letra z, es todo aquel que tiene la siguiente forma:
$ z=a+bi$
Son números que están formados de dos partes, la primera, representada por a, es un número real, y la segunda es una parte imaginaria, representada por bi, que como ya vimos, es el producto de un número real por el número i. Un ejemplo sencillo de número complejo es 4-2i, que consta de la parte real 4, y de la parte imaginaria –2i.
Los números complejos se pueden representar en el plano cartesiano; en el eje horizontal representaremos la parte real, y en el eje vertical la parte imaginaria. En la siguiente gráfica se representan los números 3+2i, y -5-4i
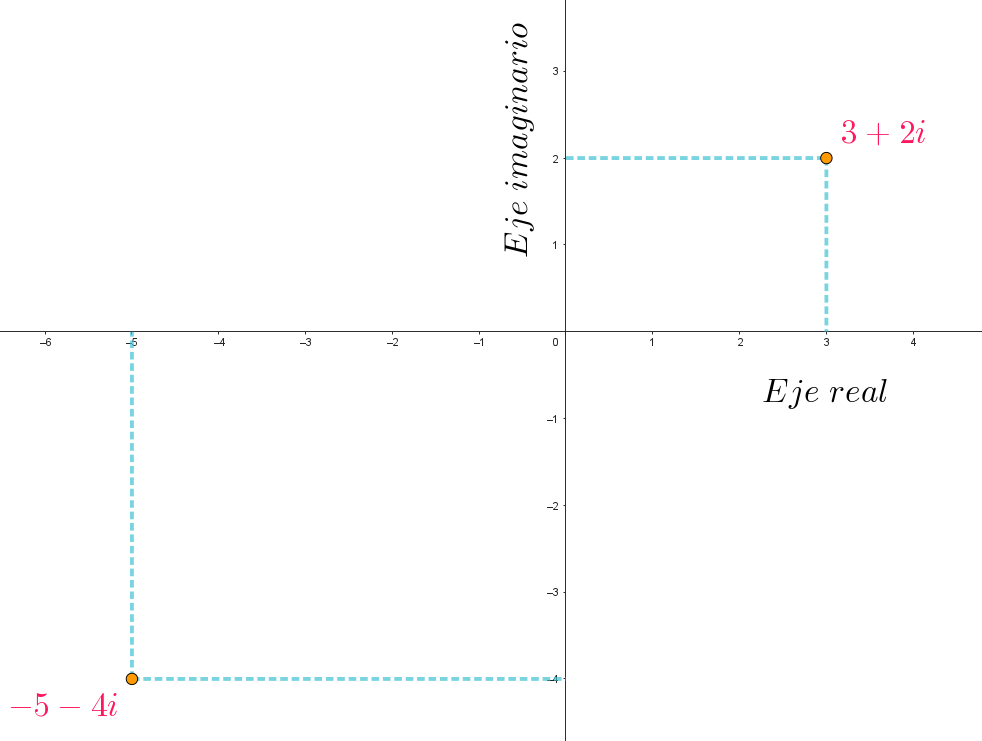
Hay más formas de representar estos números, pero esta es la más simple y sencilla de comprender.
Hay todo un sistema algebraico de números complejos: podemos sumarlos, restarlos, multiplicarlos, dividirlos y más, y como siempre pasa, los números complejos se usan en muchas cosas: una de ellas es la solución de ecuaciones de segundo grado, otra más es ayudarnos a representar de forma algebraica la corriente eléctrica, y muchas más.
Esto es lo básico que hay que saber sobre los números complejos, en realidad son sencillos y nos ayudan mucho en nuestras vidas aunque no parezca (imagínense como sería la vida sin electricidad). !Un abrazo humanos!
