Sistemas de medición angular.
¡Hola humanos! ¿Cómo están? Vamos hoy a conocer los dos principales sistemas de medición de ángulos, de dónde provienen, y en qué situaciones es mejor uno u otro.
Primero ¿qué es eso de sistema de medición angular?
Medir es comparar un objeto o fenómeno que nos interese, con una unidad de medida que ya ha sido antes definida. En términos simples consiste en ver «cuántas veces cabe» una cosa en un modelo. Por ejemplo, el humano que escribe esto, mide 1.82 metros, esto quiere decir que mide una unidad completa y 0.82 partes más de otra, de modo que 1m+0.82m=1.82m.
Ahora, en vez de comparar una longitud (la estatura), contra un patrón (el metro), vamos a girar. Vamos a empezar tomando de referencia un giro completo y vamos a dividir este giro en partes iguales. Dependiendo del número de partes en que dividamos al giro, estaremos obteniendo diferentes sistemas de medición angular.
Sistema de medición centesimal.
Este sistema consiste en dividir un giro completo en 400 partes; cada una de ellas se conoce como grado centesimal. No vamos a profundizar en él porque casi nadie (o nadie) lo usa.
Sistema de medición sexagesimal.
En este sistema dividimos un giro completo en 360 partes iguales, llamadas grados sexagesimales, o simplemente grados. Este es el sistema que más se usa en la geometría plana, o en la vida común. Un transportador común utiliza este sistema de medición.
Sistema de medición circular.
Este sistema se obtiene de crear un arco de circunferencia que tiene igual longitud que su radio, aunque suena confuso, es sencillo: imagina que trazamos una circunferencia de, por ejemplo, 3 unidades de radio, y que sobre ella trazamos un arco de también 3 unidades:
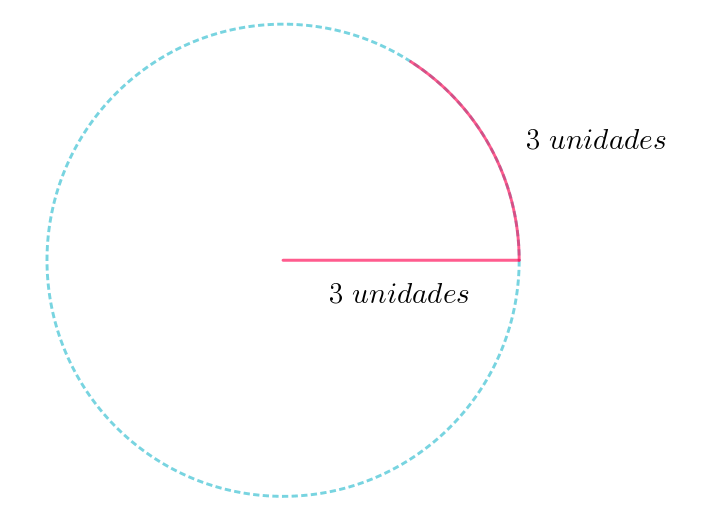
En realidad que el radio mida 3, 5, 15 o 100 unidades no importa, lo que importa es que el arco mida lo mismo que el radio, sólo usamos el 3 como ejemplo sencillo. Ahora vamos a cerrar esta región y a medir cuál es el ángulo que se ha formado:
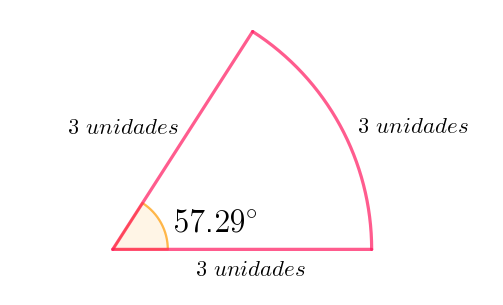
Este ángulo que se ha formado de 57.29 grados sexagesimales es el ángulo base de lo que se conoce como un radián. Entonces, un radián mide estos 57.29 grados, pero como esta equivalencia es algo molesta, se utiliza mejor esta otra:
$180{}^\circ =\pi rad$
Esto quiere decir que un ángulo llano, mide 180 grados sexagesimales, o también 3.141592… radianes.
Probablemente estén pensando humanos, que el radián tiene poco sentido, pero el radián es mejor que el grado cuando queremos trazar gráficas de funciones trigonométricas en el plano cartesiano, y por eso se le usa tanto.
El humano y sus michis esperamos que les sea útil humanos, les dejamos un ejercicio para que practiquen: conviertan el ángulo mostrado a unidades del sistema circular ¡Que estén todos bien!

