¡Saludos humanos! Ahora El esclavo y sus michis les vamos a explicar qué son las razones y proporciones y en qué las podemos utilizar en el ámbito del álgebra.
Desde que cursamos la educación más básica nos enseñaron que los números fraccionarios son una forma de expresar una división, como el siguiente:
$\frac{2}{10}$
Que de forma muy simple nos está preguntando ¿cuántas veces cabe el 2 en el10? La respuesta es que cabe 5 veces, porque:
$2\times 5=10$
A las divisiones en forma de fracción, en las que comparamos dos números también las llamamos razones. El número de arriba es el antecedente, numerador o dividendo, y el número de abajo es el consecuente, denominador o divisor:

En pocas palabras, razón es sinónimo de fracción.
Volvamos por un momento a la razón $\frac{2}{{10}}$: si la reducimos a su expresión mínima, el resultado es:
$\frac{{\cancel{2}}}{{\cancel{{10}}}}=\frac{1}{5}=0.2$
El resultado 0.2 es la comparación entre el numerador y el denominador y quiere decir que el antecedente vale solo 0.2 de lo que vale el consecuente (o si lo quieren ver también así, el consecuente vale 5 veces más que el antecedente). Vamos a ver dos ejemplos para que quede más claro esto. En el primero, vamos a analizar la razón $\frac{1}{2}$: imagina que tú tienes un gatito gris y una de tus amistades dos gatitas calicó:
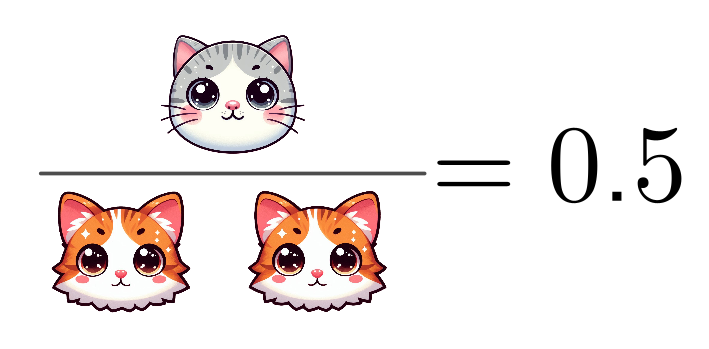
En este ejemplo, el resultado nos dice que el valor del antecedente equivale a la mitad (0.5) del valor del consecuente, o lo que es lo mismo, tienes la mitad de gatitos que tu amistad, o también, tu amistad tiene el doble de gatitas que tú. En el segundo ejemplo vamos ahora a considerar que tú tienes 4 gatitos y tu amistad 3, que es la razón $\frac{4}{3}$:
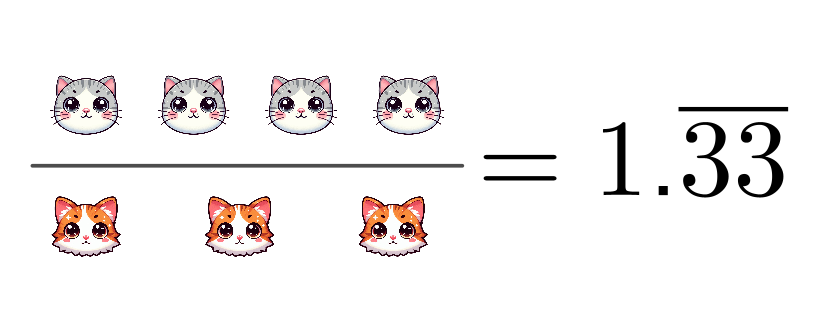
Que podemos interpretar como que tú tienes 1.33 veces más gatos que tu amistad, es algo así como decir que por cada gatita que tiene tu amistad, tú tienes 1.33 gatos; claro que en la vida real no se pueden tener fracciones de gato, pero lo que nos interesa de las razones es la comparación entre el antecedente y el consecuente.
¿Y qué son las proporciones entonces?
Una proporción es la igualdad entre dos razones; supón dos razones cualesquiera $\frac{a}{b}$ y $ \frac{c}{d}$; si las igualamos obtendremos la proporción:
$ \frac{a}{b}=\frac{c}{d}$
Que se lee «a es a b, como c es a d». Las proporciones tienen los siguientes elementos:
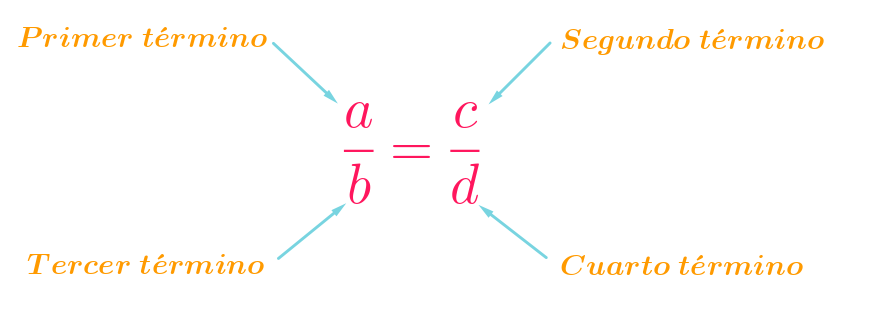
Los términos primero y cuarto se llaman extremos, y los términos segundo y tercero se llaman medios.
Supongamos ahora que en una proporción conocemos los dos términos de una de las razones, y que de la otra razón solo conocemos uno; si al término desconocido lo tratamos como una incógnita, tendríamos así una ecuación de primer grado y podríamos encontrar el valor del término desconocido. Como ejemplo vamos a encontrar el valor de la incógnita en la siguiente proporción:
$\frac{2}{7}=\frac{5}{x}$
Primero veamos qué es lo que vamos a obtener si resolvemos la ecuación: la razón de la izquierda tiene un valor de:
$\frac{2}{7}=0.285$
Cuando resolvamos la ecuación encontraremos el valor del consecuente de la razón de la derecha, que haga que ésta también valga 0.285.
Las ecuaciones fraccionarias se resuelven por medio de lo que se llama producto cruzado: multiplicamos los extremos por un lado, y los medios por otro:
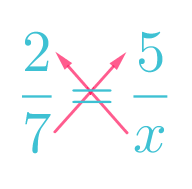
Dando como resultado parcial lo siguiente:
$\begin{array}{c}\left( 2 \right)\left( x \right)=\left( 5 \right)\left( 7 \right)\\2x=35\end{array}$
Y terminamos dividiendo entre 2 ambos miembros de la ecuación, o lo que es lo mismo «el 2 que está multiplicando en el miembro izquierdo, pasa dividiendo al miembro derecho»:
$ \displaystyle x=\frac{{35}}{2}$
La proporción ya sin incógnitas es la siguiente:
$ \frac{2}{7}=\frac{5}{{\tfrac{{35}}{2}}}$
Y comprobamos que las dos razones de la proporción son iguales porque:
$ \frac{5}{{\tfrac{{35}}{2}}}=0.285$
Estas ecuaciones que formamos de igualar dos razones, nos permiten resolver problemas de figuras geométricas semejantes, sobre todo en un teorema que se conoce como Teorema de Tales.
En esto consisten básicamente las razones y las proporciones humanos, los michis y El Esclavo esperamos que esta información les ayude. Cuídense y practiquen.
