¡Humanos! Los michis y el esclavo les vamos ahora a hablar de un concepto fundamental para el cálculo: el de límite de una función.
Para explicar de forma muy simplificada en qué consiste un límite, imaginen humanos, que la gráfica de una función es algo así como un camino, paso o carretera, imaginen también que caminan por ella; de pronto, a lo lejos observan que hay un hueco, y se acercan con curiosidad porque quieren saber qué hay en él. Aquí viene en qué consiste el límite: se pueden acercar mucho, hasta se podrán asomar y ver qué hay dentro, pero si se acercan demasiado, caerán en él.
Este ejemplo tan simplificado plantea en qué consiste el límite de una función: nos podemos aproximar mucho a una región en la que la función no existe (el hueco), y nos asomamos todo lo que se pueda para ver qué hay (el límite), sin caer y rompernos las piernas.
En nuestra entrada sobre funciones mencionamos que éstas son relaciones entre los elementos de dos conjuntos, uno que es la variable independiente, al que llamaremos el conjunto A, y el otro que es la dependiente, al que llamaremos el conjunto B. Mencionamos también que estos dos conjuntos se relacionan por medio de una regla de correspondencia, que es la expresión matemática que nos dice qué operaciones haremos con los elementos de A, para obtener los valores de B que les corresponden, por ejemplo, si la regla de correspondencia es $ f\left( x \right)=\frac{1}{{{{x}^{2}}}}$, y el valor de x es 2, entonces el valor f(2) que le corresponde es:
$ f\left( 2 \right)=\frac{1}{{{{{\left( 2 \right)}}^{2}}}}=\frac{1}{4}$
Así es como encontramos el par ordenado $\left( {2,\tfrac{1}{4}} \right)$; y que se encuentra en la gráfica de la función:
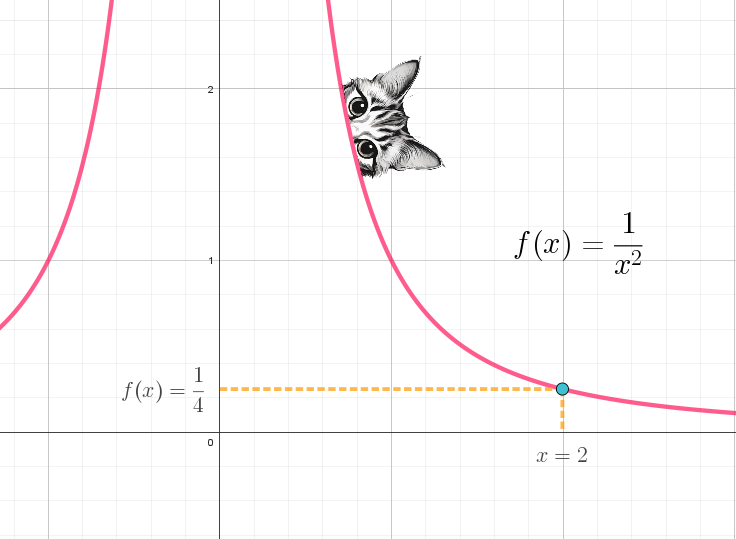
esto puede repetirse con casi cualquier valor de x, y decimos casi porque puede haber uno o más huecos, por ejemplo, en esta misma función evaluemos x=0
$ f\left( 0 \right)=\frac{1}{{{{{\left( 0 \right)}}^{2}}}}=\frac{1}{0}$
Y la división entre cero no está definida, por lo que este par ordenado no existe para esta función, lo que quiere decir que en x=0 hay un hueco (o lo que es lo mismo, la función no existe en x=0); sin embargo, nos podemos asomar al hueco. La gráfica siguiente es de la misma función pero vista desde «más lejos»:
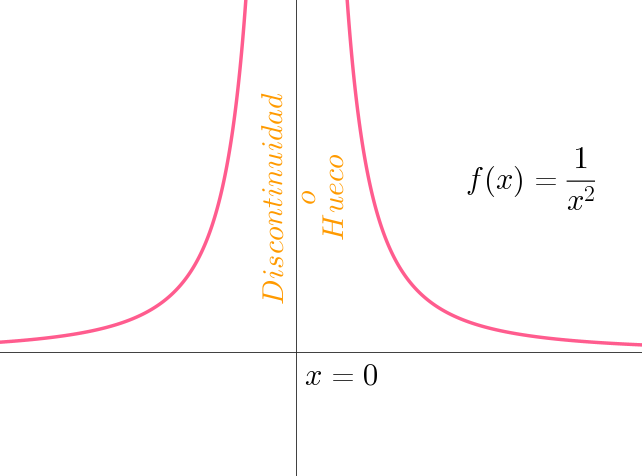
Observen que la gráfica de esta función «sube» de forma muy exagerada cuando los valores de x se acercan mucho a cero, y en exactamente x=0 encontramos un hueco, la pregunta es ¿qué hay o qué puede observarse en este hueco? La gráfica asciende tanto, que podemos afirmar que cuando x tiene un valor de cero, el valor de f(x) es tan grande que prácticamente alcanza el infinito.
El infinito no es un número, simplemente porque hay infinitos de diferentes tamaños por raro que suene, por ejemplo, los números enteros son infinitos, y también lo son todos los enteros positivos; ambos conjuntos de números son infinitos pero uno es más grande que el otro. Entonces, como no podemos establecer de forma exacta este valor de f(x), solo lo estimamos o aproximamos por medio de un límite; entonces, en lugar de escribir un hipotético par ordenado $ \left( {x,\infty } \right)$, que de hecho es incorrecto, lo hacemos con la notación de límite:
$\lim\limits_{x \to 0} \frac{1}{x^2}=\infty$
Que se lee como «el límite de la función $ f\left( x \right)=\tfrac{1}{{{{x}^{2}}}}$ cuando x tiende a cero, es igual a infinito». La forma en la que se expresa esto de manera general es la siguiente:
$ \lim\limits_{x \to a} f(x)=L$
Desde el punto de vista práctico, encontrar un límite es muy parecido a evaluar una función. Por ejemplo, evaluemos el límite cuando x tiende a 1 si función es $ f\left( x \right)=\tfrac{{{{x}^{2}}-4}}{{x-2}}$:
$\lim\limits_{x \to 1}\left( {\frac{{{{x}^{2}}-4}}{{x-2}}} \right)=\frac{{{{{\left( 1 \right)}}^{2}}-4}}{{\left( 1 \right)-2}}=3$
Evaluamos como siempre, y encontramos que el par ordenado (1,3) forma parte de la función, perfecto. ¿Y si x es igual a 2 qué pasa?
$\lim\limits_{x \to 2}\left( {\frac{{{{x}^{2}}-4}}{{x-2}}} \right)=\frac{{{{{\left( 2 \right)}}^{2}}-4}}{{\left( 2 \right)-2}}=\frac{0}{0}$
En este caso no es tan fácil identificar el valor de f(x) que corresponde a x=2; se debe hacer una serie de manipulaciones algebraicas hasta obtener el resultado, que interpretaríamos como el par o pares ordenados que no forman parte de la función.
El concepto de límite es muy importante, no solo por las aplicaciones prácticas que tiene, sino porque otros conceptos como el de derivada y el de integral definida se construyen con él.
El esclavo y los michis esperamos que esta entrada les haya ayudado humanos. Cuídense, estudien y supérense ¡abrazos!
